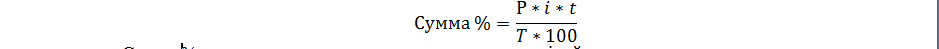Что такое процент? формула процентов. проценты — как считать?

Как искать процент от числа

Кредиты банков Уфы

Формула сложных процентов.

Она применяется реже в депозитной практике банка, но такие предложения найти можно. Для большинства вкладчиков они  не являются привлекательными по причине того, что ставки по ним ниже, чем по продуктам, когда доход начисляется  только по окончании действия депозитного договора. Периодичность присоединения дохода может быть разной: раз в месяц, раз в неделю, раз в квартал, каждый год. Она подразумевает под собой капитализацию или начисление «процентов на проценты».

Формула сложных %-ов:

P – изначальная сумма вклада.

i – депозитная годовая ставка.

k – число дней в периоде, через который начисляется доход.

T – число дней в году.

n – число капитализаций дохода в течение всего срока депозита.

Рассмотрим пример №1: разместим 100 000 рублей под 12% годовых на полгода с ежемесячной капитализацией.
Полученное значение подтвердим через расчеты в Excel.

Таким образом, благодаря ежемесячной капитализации, общий итог вложений оказался выгоднее, чем в варианте, когда проценты причисляются  в конце срока.

Пример №2: разместим 100 000 рублей на 6 месяцев под 12% годовых с еженедельной капитализацией.

Полученное значение подтвердим через расчеты в Excel.

Пример №3: разместим 100 000 рублей на 1 год под 12% годовых с ежеквартальной капитализацией.

Полученное значение подтвердим через расчеты в Excel.

Пример №4: разместим 100 000 руб на 1 месяц под 12% годовых с ежедневной капитализацией.

Полученное значение подтвердим через расчеты в Excel.

Таким образом, капитализация и формула сложных процентов дает более выгодный эффект, поэтому, при размещении денег в банке не стоит упускать из виду подобные варианты размещения.

Бесполезно
11

Занятно
13

Помогло
25

ПСК

Полная стоимость кредита — это и есть та самая величина, отражающая все затраты заемщика, которые он понесет в процессе уплаты основного долга по кредиту. Раньше эту информацию банк старался умалчивать, дабы клиент не передумал оформлять кредит. Однако, согласно закону от 2014 года, банк обязуется указывать эту сумму на первой странице кредитного договора и на обязательном графике платежей. Причем размер этой записи должен быть максимально большим, дабы избежать дальнейших недоразумений.

Рассчитать этот показатель можно по простой формуле:

ПСК=СК+СВК+%, где:

• СК — сумма кредита;
• СВК — сумма всех комиссий (разовых и ежемесячных);
• % — проценты по кредиту.

Деление числа на 100

При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем: Переведем 15% в рубли: 250 : 100 = 2,5 — это 1% от стоимости шоколада, значит 2,5 * 15 = 37,5 — это 15%. 250 — 37,5 = 212,5. 212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Составление пропорции

Пропорция — определенное соотношение частей между собой. 

С помощью метода пропорции можно рассчитать любые %. Выглядит это так:

a : b = c : d. 

Читается: а относится к b так, как с относится к d

Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение

Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Как решаем: Узнаем сколько стоит футболка сейчас в % соотношении: 100 — 14 = 86, значит 1390 рублей это 86%. Составим пропорцию: 1390 : 100 = х : 86, х = 86 * (1390 : 100), х = 1195,4. 1390 — 1195,4 = 194,6.

Ответ: купить спортивную футболку выгоднее на 194,6 рубля.

Отзывы о Альфа банк Уфа

Методы решения

Математики представляют величину целым, т.е. в ней полные 100%, а какая-то доля заданной величины – это ее сотая часть. Таким образом, процент — это сотая часть от какого-то полного значения. Например, 1 килограмм – это 100%, а полкилограмма – это 50%.

Определить процент от числа удобно с помощью пропорций. Пусть необходимо будет взять и найти 1 процент от цифры 349, где:

349 = 100%;

х = 1%.

Тут следует быть внимательными, поскольку можно запутаться, что есть что. Чтобы этого избежать, следует всегда писать доли (%) с одной стороны. Лучше всего составлять пропорцию в столбик — определить процент от числа тогда будет удобнее. Найдем х с помощью правила креста:

х = 349*1

х = 349/100

х = 3,39.

Основные формулы

Существует несколько основных формул для решений уравнений с долями.

Как посчитать процент от числа? Если известна величина Х, а определить надо величину Q, которая составляет долю, то представить выражение следует дробью:

Y = X*Q/100%

Как найти число по его доле? Если известна величина X, которая составляет несколько долей от Y, а найти необходимо значение неизвестного Y, то выражение решается с помощью формулы:

Y = X*100%/Q

Q = Y/X*100%

Эти три формулы наиболее часто встречаются при решении различных уравнений с долями, поэтому важно запомнить их и научится быстро применять

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби.

• 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
• 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
• 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
• 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
• 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100 — 25 = 75, значит нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 8500 : 4 * 3 = 6375.

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Использование калькуляторов

Современные технологии позволяют не высчитывать проценты от чисел самостоятельно, воспользовавшись техникой. Можно использовать обычный электронный калькулятор с процентами. Чтобы убедиться, что устройство подходит, необходимо найти на нем кнопку с изображением %, такие обычно находятся среди действий умножения-деления. После этого можно приступать к расчетам.

Как находить проценты от числа? Например, величину, которая составляет 17% от цифры 123. Используя калькулятор, можно рассчитать:

1. Набрать 123, так чтобы оно отобразилось на табло.
2. Выбрать действие умножить (значок Х).
3. Затем ввести 17 и нажать на соответствующую кнопку (%).
4. На табло высветится ответ — 20,91.

Данный алгоритм используется для нахождения ответов на любые выражения с расчетами долей и сотых. Но еще один удобный метод – это использование онлайн-калькулятора. Для решения задачи достаточно перейти на сайт такого калькулятора, введя его адрес в строку браузера или прописав запрос в поисковой системе.

Онлайн-калькулятор представляет собой страницу сайта, где есть окошки, куда необходимо вводить значения. Обычно перед окошком пишется, какое действие выполняет калькулятор (находит % от количества, количество по % и т. д.), поэтому надо правильно выбрать. Достаточно ввести значения в соответствующие окна и кликнуть на кнопку «Решить» («Найти», «Рассчитать» и т.д.), калькулятор выдаст ответ.

Основные определения

Процент — это одна сотая часть от любого числа. Обозначающим знаком является %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить известное на 100, как в примере выше.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например, 0,18 = 0,18 · 100% = 18%. Как перевести проценты в десятичную дробь — обратным действием: 18 : 100 = 0,18.

Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а далее используем предыдущее правило.

Развивайте математическое мышление детей на наших уроках математики вместе с енотом Максом и его друзьями. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее подружиться со школьной математикой.

Расчет процентов на банковский депозит. Формула расчета простых процентов.

Если проценты на депозит начисляются один раз в конце срока депозита, то сумма процентов вычисляется по формуле простых процентов.

S = K + (K*P*d/D)/100 Sp = (K*P*d/D)/100

Где: S — сумма банковского депозита с процентами, Sp — сумма процентов (доход), K — первоначальная сумма (капитал), P — годовая процентная ставка, d — количество дней начисления процентов по привлеченному вкладу, D — количество дней в календарном году (365 или 366).

Пример 1. Банком принят депозит в сумме 100 тыс. рублей сроком на 1 год по ставке 20 процентов.

S = 100000 + 100000*20*365/365/100 = 120000 Sp = 100000 * 20*365/365/100 = 20000

Пример 2. Банком принят депозит в сумме 100 тыс. рублей сроком на 30 дней по ставке 20 процентов.

S = 100000 + 100000*20*30/365/100 = 101643.84 Sp = 100000 * 20*30/365/100 = 1643.84

Как посчитать проценты: примеры

Типы задач на проценты

В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.

Тип 1. Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?

Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).

20% = 0,2

500 * 0,2 = 100

Из общего количества изготовленных стульев контроль не прошли 100 штук.

Тип 2. Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.

Задача. Школьник решил 38 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 38 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.

38/0,16 = 38 * 100/16 = 237,5

Значит 237 задачи включили в этот сборник.

Тип 3. Нахождение процентного отношения двух чисел

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.

Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?

Как решаем: возьмем алгоритм из правила выше:

10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 47%

В классе учится 10 девочек — это 47%.

Тип 4. Увеличение числа на процент

Чтобы увеличить число на некоторое количество процентов, нужно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.

Формула расчета процента от числа выглядит так:

a = b * ((1 + c) / 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом месяце стикер-пак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?

Как решаем: подставим в формулу данные из условий задачи.

110 * (1 + 12/100) = 110 * 1,12 = 123,2.

Стоимость стикер-пака в этом месяце — 123 рубля 20 копеек.

Тип 5. Уменьшение числа на процент

Чтобы уменьшить число на несколько процентов, нужно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.

Формула расчета выглядит так:

a = b * ((1 — c) / 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом году школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?

Как решаем: подставим в формулу данные из условий задачи.

100 * (1 – 25/100) = 75

75 выпускников закончат школу в этом году.

Тип 6. Задачи на простые проценты

Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.

Формула расчета выглядит так:

S = а * ((1 + у * х)/ 100),

где a — исходная сумма,

S — сумма, которая наращивается,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Родители взяли в банке кредит 5000 рублей, чтобы купить тебе что-то классное. Кредит на год под 15% ежемесячно. Сколько денег они внесут через год?

Как решаем: подставим в формулу данные из условий задачи.

5000 * (1 + 12 * 15/100) = 14000

Родители через год внесут в банк 14000 рублей.

Тип 7. Задачи на сложные проценты

Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.

Формула расчета выглядит так:

S = а * ((1 + х)/100)y,

где S — наращиваемая сумма,

a — исходная,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Папа взял в банке кредит 25000 рублей на 3 месяца под 15%. Нам нужно узнать, сколько денег придется заплатить банку по истечении срока кредита.

Как решаем: просто подставим в формулу данные из условий задачи:

25000 * (1 + 15/100)3 = 38021,875 — искомая сумма.

Способы нахождения процента

Универсальная формула для решения задач на проценты:

A * b = C, где A — исходное число, b — проценты, переведенные в десятичную дробь, C — новое число.

Чтобы применить алгоритм, нужно прочитать задачу, отметить, какие два числа нам известны и найти третье.

Есть еще четыре способа поиска процентов. Рассмотрим каждый из них.

Простые и сложные проценты

Инвесторы, которые работают на рынке Форекс, сталкиваются с повторным вложением денег (реинвестированием) постоянно. Если банковские депозиты приносят владельцам прибыль через несколько месяцев или даже год, то на валютном рынке прибыль/убыток появляется после каждой сделки.

Поэтому все, кто интересуется инвестициями на Форексе, будут регулярно работать с простыми и сложными процентами. Давайте же разберемся, что же означают эти понятия.

Простой процент используется в случаях, когда база начисления процентов всегда равна начальной сумме вложений. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.

Каждый раз, когда инвестор хочет несколько раз «прокрутить» свои деньги через инвестиционный инструмент, он сталкивается со сложным процентом. Полученная прибыль на первом круге реинвестируется и проценты уже начисляются на более крупную сумму.

В инвестициях на рынке Форекс сложный процент используется постоянно, потому что сумма вложений меняется после каждой сделки. Многие инвесторы используют тактику «вложил и забыл», оставляя полученную прибыль работать вместе со стартовым вкладом.

Разница между простыми и сложными процентами на первый взгляд кажется не такой уж большой. Но чем больше проходит времени, тем очевиднее становится преимущество сложных процентов:

Простые и сложные проценты на одном графике

Конечно, это всё теория и на практике добиться 30-кратного реинвестирования прибыли совсем непросто. Но факт остаётся фактом — сложные проценты могут сослужить хорошую службу инвестору. И чтобы умело их использовать, нужно правильно их считать, в чём помогут несколько полезных формул.

Как найти процентное соотношение чисел

Также могут возникнуть ситуации, когда нужно высчитать процентное соотношение двух чисел. К примеру, какой процент число B составляет от числа А, на сколько процентов (B) вы выполнили свою работу от заданной нормы (A), на сколько (B) повысилась цена товара от первоначальной (A) и так далее.

Для определения такого результата существуют следующая формула:

B / A * 100 =

К примеру, нам нужно высчитать, какая доля от числа 500 составляет число 85.

Используя приведённую формулу, выполняем несложные арифметические операции:

85 / 500 * 100 = 17%

Таким образом, число 85 составляет 17% от 500.

Проверяем полученное число по формуле первого способа:

500 / 100 * 17 = 85.

Всё сошлось.

Расчет процентов

Для начисления процентной ставки банки используют два метода: аннуитетный и дифференцированный. Основное отличие каждого из методов в скорости выплаты процентов по кредиту.

Дифференцированные платежи предполагают уплату ежемесячного платежа в разной сумме на протяжении всего срока действия кредитного договора, при котором в первую очередь выплачиваются проценты банку, а ближе к концу кредитного соглашения погашается основная сумма задолженности. Стоит отметить, что проценты насчитываются каждый раз на остаток кредитного долга. Для расчета такого способа оплаты кредита используют формулу:

Сумма платежа = остаток по займу*% по кредиту*количество дней/100/365

Онлайн калькулятор

Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так:

• Для подсчета % от суммы: вводим известное, равное 100%, знак умножения, нужный процент, знак %.
• Чтобы вычесть %: введем известное, равное 100%, знак минус, размер процентной доли и знак %.

5 класс, урок в самом разгаре, нужно определить процент от числа как можно быстрее — поможет онлайн калькулятор. Составлять расчет быстро и точно:

• Раз
• Два
• Три
• Четыре

Но помните, что на контрольных работах и экзаменах за вас никто не решит, а калькулятор не поможет.

Приходите практиковаться! В детской школе Skysmart ученики разбирают интересные задания, проходят квесты, играют в английский на интерактивной платформе и обсуждают темы, которые им интересны. Никаких скучных упражнений — только то, что зажигает вашего ребенка. Запишите его на бесплатный вводный урок и покажите, что английский может быть увлекательным путешествием!

Расчет банковских процентов по вкладам — формула

Исходя из положений п. 1 ст. 838 Гражданского кодекса Российской Федерации (ГК РФ), формула расчета банковских процентов по вкладам зависит от того, как процент по вкладу определен в соглашении сторон.

Так, если процент прямо в договоре не установлен, то с учетом п. 1 ст. 809 ГК РФ он определяется на основании ставки банковского процента по месту нахождения вкладчика на дату выплаты денег. При этом особенности расчета процента могут иметь место в зависимости от того, открыт классический вклад или заведена сберегательная книжка, приобретен ли сберегательный сертификат.

Помимо собственно размера процента, для произведения расчета необходимо определить период, за который начисляются проценты, а также сумму, на которую они начисляются (включает она начисленные ранее проценты или ограничивается изначально внесенной суммой).

ВАЖНО! Согласно п. 1 ст. 839 ГК РФ день внесения банковского вклада для расчета процентов не учитывается, в то время как день выдачи денег включается в расчет.

В соответствии с п. 2 указанной статьи проценты выплачиваются ежеквартально или входят в общую сумму для расчета последующих процентов, если не были востребованы вкладчиком. Иной порядок может быть определен соглашением сторон.

Что такое прогрессивное начисление по банковскому вкладу

Прогрессивное начисление как таковое используется в праве не только применительно к банковским вкладам.

Так, при взыскании денежных средств, присуждаемых за неисполнение судебного акта, в судебной практике, в частности, встречается такой подход, как установление прогрессивного начисления. Например, если за каждый последующий период неисполнения взыскивается сумма больше, чем предполагалась за неисполнение в менее продолжительные периоды просрочки (постановление 18-го арбитражного апелляционного суда от 26.06.2015 № 18АП-6587/2015 по делу № А07-4912/2014).

Применительно к банковским вкладам прогрессивное начисление может означать, например, отличие размера процентов в зависимости от суммы остатка на депозите (письмо Минфина РФ от 05.12.2011 № 03-04-06/6-332). Помимо роста ставки с ростом суммы на депозите, прогрессивное начисление процентов по вкладу может применяться в зависимости от срока вклада, например увеличение процентной ставки при превышении годичного срока вклада.

Прогрессивное начисление по банковскому вкладу как нарастание ставки в зависимости от времени, когда вклад востребуется вкладчиком, признается экспертами в качестве одного из механизмов, используемых банками для снижения рисков в своей профессиональной деятельности (п. 5 экспертного заключения по проекту Федерального закона «О внесении изменений в ст. 837 ГК РФ», принятого на заседании Совета при Президенте РФ по кодификации и совершенствованию гражданского законодательства 17.11.2003).

Процент от — Таблица для 10000

Процент от	Разница
1% от 10000 это 100	9900
2% от 10000 это 200	9800
3% от 10000 это 300	9700
4% от 10000 это 400	9600
5% от 10000 это 500	9500
6% от 10000 это 600	9400
7% от 10000 это 700	9300
8% от 10000 это 800	9200
9% от 10000 это 900	9100
10% от 10000 это 1000	9000
11% от 10000 это 1100	8900
12% от 10000 это 1200	8800
13% от 10000 это 1300	8700
14% от 10000 это 1400	8600
15% от 10000 это 1500	8500
16% от 10000 это 1600	8400
17% от 10000 это 1700	8300
18% от 10000 это 1800	8200
19% от 10000 это 1900	8100
20% от 10000 это 2000	8000
21% от 10000 это 2100	7900
22% от 10000 это 2200	7800
23% от 10000 это 2300	7700
24% от 10000 это 2400	7600
25% от 10000 это 2500	7500
26% от 10000 это 2600	7400
27% от 10000 это 2700	7300
28% от 10000 это 2800	7200
29% от 10000 это 2900	7100
30% от 10000 это 3000	7000
31% от 10000 это 3100	6900
32% от 10000 это 3200	6800
33% от 10000 это 3300	6700
34% от 10000 это 3400	6600
35% от 10000 это 3500	6500
36% от 10000 это 3600	6400
37% от 10000 это 3700	6300
38% от 10000 это 3800	6200
39% от 10000 это 3900	6100
40% от 10000 это 4000	6000
41% от 10000 это 4100	5900
42% от 10000 это 4200	5800
43% от 10000 это 4300	5700
44% от 10000 это 4400	5600
45% от 10000 это 4500	5500
46% от 10000 это 4600	5400
47% от 10000 это 4700	5300
48% от 10000 это 4800	5200
49% от 10000 это 4900	5100
50% от 10000 это 5000	5000
51% от 10000 это 5100	4900
52% от 10000 это 5200	4800
53% от 10000 это 5300	4700
54% от 10000 это 5400	4600
55% от 10000 это 5500	4500
56% от 10000 это 5600	4400
57% от 10000 это 5700	4300
58% от 10000 это 5800	4200
59% от 10000 это 5900	4100
60% от 10000 это 6000	4000
61% от 10000 это 6100	3900
62% от 10000 это 6200	3800
63% от 10000 это 6300	3700
64% от 10000 это 6400	3600
65% от 10000 это 6500	3500
66% от 10000 это 6600	3400
67% от 10000 это 6700	3300
68% от 10000 это 6800	3200
69% от 10000 это 6900	3100
70% от 10000 это 7000	3000
71% от 10000 это 7100	2900
72% от 10000 это 7200	2800
73% от 10000 это 7300	2700
74% от 10000 это 7400	2600
75% от 10000 это 7500	2500
76% от 10000 это 7600	2400
77% от 10000 это 7700	2300
78% от 10000 это 7800	2200
79% от 10000 это 7900	2100
80% от 10000 это 8000	2000
81% от 10000 это 8100	1900
82% от 10000 это 8200	1800
83% от 10000 это 8300	1700
84% от 10000 это 8400	1600
85% от 10000 это 8500	1500
86% от 10000 это 8600	1400
87% от 10000 это 8700	1300
88% от 10000 это 8800	1200
89% от 10000 это 8900	1100
90% от 10000 это 9000	1000
91% от 10000 это 9100	900
92% от 10000 это 9200	800
93% от 10000 это 9300	700
94% от 10000 это 9400	600
95% от 10000 это 9500	500
96% от 10000 это 9600	400
97% от 10000 это 9700	300
98% от 10000 это 9800	200
99% от 10000 это 9900	100
100% от 10000 это 10000

Формулы сложных процентов по вкладам и примеры решения задач

Формулы сложных процентов в математике встречаются постоянно, особенно если речь идёт об экономических задачах. Представьте, что вам нужно рассчитать прибыль от банковского вклада за несколько лет. Для этого понадобится такая информация:

• начальная сумма вклада (K нулевая или К)
• ставка доходности (R) — переводится из процентов в число (10% = 0.1)
• количество периодов реинвестирования, то есть лет (n)

А конечную сумму вклада мы назовем просто K. Её можно рассчитать по формуле:

Конечная сумма при расчёте сложных процентов по вкладу

Пример задачи: Инвестор П. положил на депозит в банке 10000$ под 10% годовых. Какую прибыль он получит через 5 лет?

Для начала, давайте узнаем конечную сумму вклада по формуле:

K = 10000$ * (1 + 0.1)5 = 16105.1$

Прибыль (P) — это разница между конечной и стартовой суммой вклада. Считаем:

P = K — К = 16105.1$ — 10000$ = 6105.1$

Можно даже подсчитать прибыль в процентах, для этого нужно найти не разницу, а отношение между конечной и стартовой суммой:

P (%) = K/К — 1 = 16105.1$ / 10000$ — 1= 61.05%

Используя формулу сложных процентов, вы всегда можете предсказать результат инвестирования в будущем. Впрочем, бывают ситуации, когда вам нужно узнать не конечную, а стартовую сумму вклада. Её можно найти по той же формуле сложных процентов по вкладам, но надо немного её изменить:

Формула расчёта сложных процентов для поиска стартовой суммы вклада

Пример задачи: Инвестор В. хочет узнать, сколько ему надо вложить рублей под 20% годовых сейчас, чтобы через 3 года стать рублёвым миллионером. 

Используем формулу:

К = 1000000₽ / (1 + 0.2)3 =  578703.7₽

Кроме суммы вклада, через формулу можно найти и остальные параметры. Например, зная стартовую и конечную сумму, можно узнать процентную ставку или количество периодов реинвестирования.

Начнем с процентной ставки:

Формула расчёта сложных процентов по вкладу для поиска нужной процентной ставки

Пример задачи: Инвестор Р. хочет выяснить, вклад с какой процентной ставкой ему нужен, чтобы заработать 10000$ за 3 года, изначально вложив 20000$.

Для начала нужно посчитать конечную сумму, так как мы знаем только прибыль:

K = К+ P = 20000$ + 10000$ = 30000$

А теперь можно использовать формулу:

R = (30000$ / 20000$) ^ 1/3 — 1 = 14.47%

Чтобы получить такую доходность, банковский депозит не подойдёт, а вот консервативный ПАММ-счёт — вполне.

Напоследок давайте выясним, как рассчитать, на какой срок нужно положить деньги, чтобы получить нужную нам прибыль. Без логарифмов не обойтись:

Расчёт сложных процентов по вкладу — поиск нужного количества периодов реинвестирования

Пример задачи: сколько лет нужно держать деньги на депозите в банке под 25% годовых, чтобы 50000 рублей превратить в 100000?

Подставляем в формулу:

n = log_1+0.25 100000/50000 = 3.11 лет

Кстати, если речь идёт о банке, то 3.11 лет округляются до 4 — вы обычно не можете снять свои деньги до окончания периода действия вклада. Условия конкретного инвестиционного инструмента всегда стоит учитывать при решении подобных задач.

Кроме рассмотренных нами задач существуют и более сложные. Например, довольно распространённая история — у инвестора есть вклад с возможностью пополнения. Часть каждой зарплаты отправляется туда и надо выяснить, какой же будет результат по итогам.

Пример задачи: Инвестор З. вложил 1000$ и откладывает 50$ каждый месяц. Процентная ставка — 1% в месяц. Какая сумма накопится через 5 лет?

Чтобы узнать результат, нужно создать табличку:

Расчёт результатов инвестирования с доливками, с учётом сложных процентов

В первый месяц сумма инвестиций составила 1000$, на неё начислен 1% — итого 1010$. Во второй месяц работают уже 1010$ и еще 50$, которые инвестор внёс дополнительно. Итого — 1070.10. И так далее…

Разумеется, считать эти таблички каждый раз — довольно напряжно, решать логарифмы — тем более. Поэтому специально для вас при помощи программы Microsoft Excel я сделал небольшой файлик для решения задач по сложным процентам.