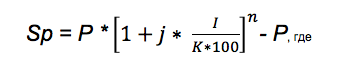Как посчитать ежемесячный платеж по кредиту

Содержание

Определение каждого типа

При аннуитетном виде ежемесячные выплаты одинаковы на протяжении установленного срока кредитования, причём сначала необходимо погасить проценты банка, а уже потом будет уменьшаться само тело кредита.

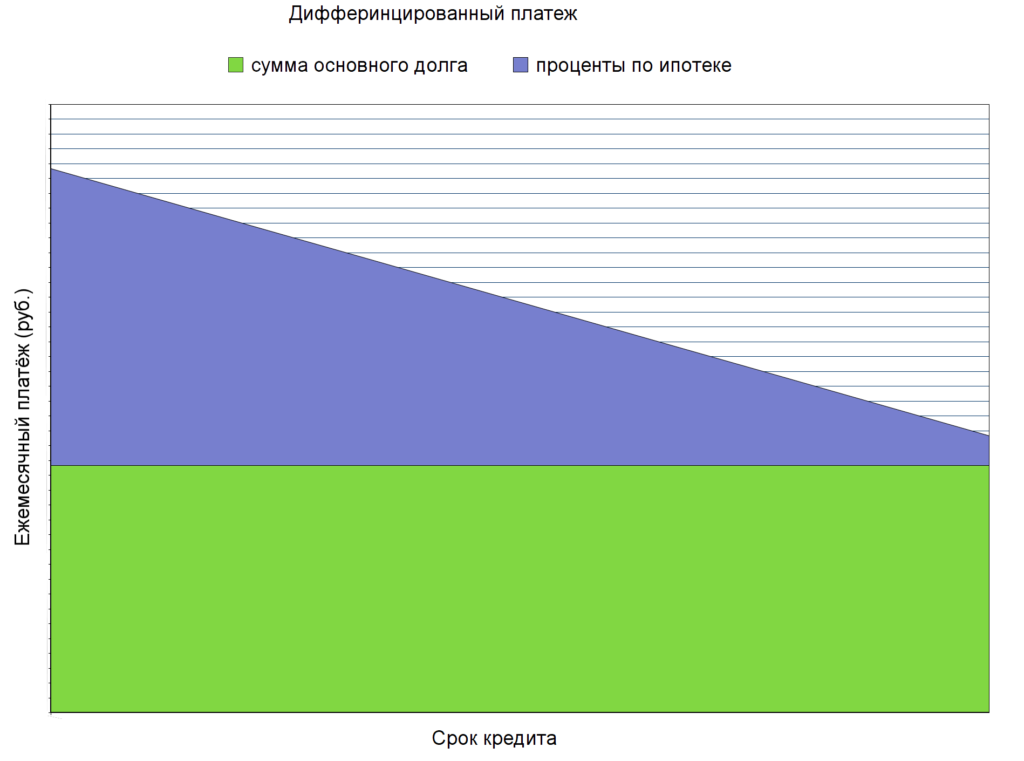
А дифференцированный платёж – это способ погашения кредита, при котором равномерно уменьшается тело кредита и проценты, начисляемые на сумму долга. Таким образом, первая выплата будет наибольшей, а в следующие месяцы гарантированно уменьшится.

Начальные платежи при дифференцированной схеме могут оказаться довольно большими, так как проценты начисляются на оставшееся тело кредита.

Какие выделяют виды аннуитета?

Для лучшего понимания использования аннуитета следует рассмотреть, какие его виды существуют. Так, можно отметить наличие следующей классификации:

• отложенный – в данном случае первая выплата производится в конце начального периода;
• немедленный – платеж осуществляется в начале нулевого периода.

Если говорить об аннуитете, используемом в сфере кредитования, то здесь имеет место отложенный аннуитет.

Кроме этого, распространенно выделение различных видов стоимости аннуитета, а именно:

• приведенная;
• будущая стоимость аннуитета.

Такое деление обусловлено стремлением определить максимально объективную ценность денежных средств, которые направлены на кредитование. Как будущая, так и текущая стоимость аннуитета рассчитывается определенным образом с использованием конкретных формул. Проводимый расчет текущей стоимости аннуитета зависит от ряда факторов.

Стоит отметить, что в силу теории о том, что с течением времени денежные средства могут обесцениваться в силу инфляции, имеет место такое понятие, как настоящая стоимость аннуитета. Также здесь играет роль упущенная выгода, ведь если бы кредитор оставил выданные денежные средства у себя, то он имел бы возможность получать доход в виде процентов по вкладу.

Thank you!

Код ОГРН: 1481/1597

Услуги

• «Колибри» (внутренние)
• «Колибри» (международные)
• MoneyGram
• Аккредитивы
• Банковские карты (дебетовые)
• Блиц-оплата (ф.190)
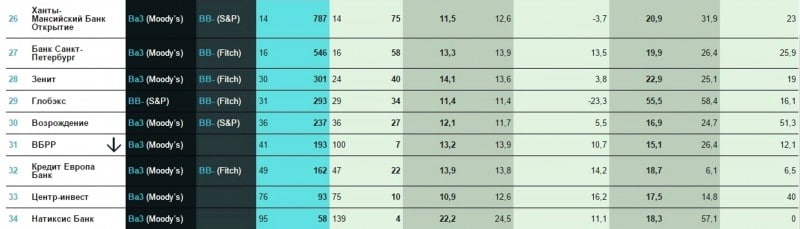
• Брокерское обслуживание
• Выдача выписок, исполнение справок по запросам клиентов
• Выдача наличных денежных средств со счета, в том числе по денежным чекам
• Депозитарное обслуживание
• Зарплатные проекты
• Зона самообслуживания 24 ч
• Инвестиционные продукты
• Ипотечные (жилищные) кредиты – консультирование (прием заявок)
• Ипотечные (жилищные) кредиты – оформление (выдача)
• Клиент-Сбербанк, СПЭД БИК IBSO, КЛИЕНТ-ИНТЕРНЕТ-БАНК (BANKFAKTURA) и другие системы
• Консалтинговые услуги по обслуживанию ВЭД и валютному контролю
• Кредитные карты
• Обезличенные металлические счета
• Обслуживание ВИП сегмента
• Обслуживание массового высокодоходного сегмента
• Обслуживание физических лиц
• Обслуживание юридических лиц
• Операции с наличной иностранной валютой
• Операции с паями ПИФ
• Оплата векселей /депозитных сертификатов
• Открытие и ведение банковских счетов клиентов в иностранной валюте
• Открытие и ведение банковских счетов клиентов в рублях
• Открытие УДБО
• Переводы в иностранной валюте
• Переводы в рублях
• Платежи в пользу ЮЛ
• Потребительские кредиты – оформление (прием документов)
• Потребительские кредиты – оформление и выдача
• Предоставление в аренду индивидуальных сейфов
• Привлечение денежных средств клиентов в виде неснижаемого остатка на банковском (расчетном) счете
• Прием денежной наличности по препроводительным документам клиента
• Прием для направления на инкассо наличной иностранной валюты
• Прием и исполнение распоряжений клиентов на бумажном носителе в валюте РФ и иностранной валюте
• Прием наличных денежных средств в валюте РФ на счет по объявлению на взнос наличными
• Продукты партнеров
• Реализация функций агента валютного контроля
• Сбербанк бизнес онлайн
• Сберегательные сертификаты Банка
• Страхование
• Торговый эквайринг
• Услуги инкассации
• Услуги НПФ Сбербанка

Досрочное погашение при аннуитетных платежах

Погасить аннуитетный кредит досрочно – проблематично и не всегда выгодно. Некоторые банки, которые предоставляют кредиты, предоставляют специальные условия для тех, кто желает оплатить кредит досрочно.

Главные преимущества досрочного погашения аннуитетных кредитов:

1. Уменьшение срока. Для тех, кто желает быстрее избавиться от ипотечного или любого другого длительного кредитования эта возможность является преимуществом. Несмотря на то что в большинстве случаев погашать кредит досрочно – не выгодно, многие заемщики выплачивают задолженность досрочно.
2. Уменьшение суммы аннуитетного платежа. Стоит заметить, что заемщик имеет возможность оплатить не полную стоимость кредита, а её часть, после чего сделав пересчет в банке и уменьшив ежемесячную обязательную плату.

Заметка! Банки часто идут на уступки и при хорошей кредитной истории предлагают заемщикам более выгодные и приемлемые условия с уменьшением процентной ставки.

Как эти расчеты могут в жизни пригодиться?

В примерах выше разобраны абстрактные примеры аннуитетов. Однако с аннуитетными денежными потоками встречаемся и в реальной жизни. К примеру, интересно будет рассчитать, сколько получится накопить на сберегательном счете, когда откладывать каждый месяц часть зарплаты. Так же можно будет рассчитать, например, дисконтированную стоимость платежей по автокредиту. Выплаты банку при приобретении автомобиля (и не только автомобиля) в кредит являют собой аннуитет. Его дисконтированная (приведенная к сегодня) стоимость  — это и будет стоимость покупаемого автомобиля. Можно узнать точно, сколько переплачиваете при покупке в кредит машины по сравнению с вариантом покупки с оплатой полной суммы сразу. А также можно будет сравнивать кредитные предложения различных банков. Единственная проблема в данных расчетах – выбрать правильную месячную ставку дисконтирования.

Вечная рента

Вечная рента — аннуитет, платежи которого длятся в течение неограниченного срока. Другими словами – это серия одних платежей, которая вечно продолжается. Такой вариант возможен, если, к примеру, у вас есть вклад в банке, вы снимаете лишь ежегодные проценты, а главная сумма вклада остается нетронутой. Тогда, когда ставка процента по вкладу не изменяется, у вас будет вечная рента.

Все английские аристократы в викторианскую эпоху жили на проценты от своего капитала. Чем больший капитал в банке лежал, тем больше средств можно было потратить на жизнь и не работать при этом. Капитал по наследству переходил, и теоретически (если бы не было инфляции, войн, банкротств банков) так могло бы продолжаться вечно.

Будущая стоимость вечной ренты смысла не имеет, так как платежи длятся неограниченно долго. Но текущая стоимость вечной ренты является конечной суммой, которую возможно вычислить по формуле:

PV = платеж/R,

где R – это банковская ставка %, PV — текущая стоимость

К примеру, когда хочется со счета снимать проценты в сумме 500,000 рублей в год, а годовая банковская ставка 8%, то это означает, что на банковском счете сумма вклада должна равняться:

500,000/0,08 = 6,250,000 рублей (PV).

В этом случае (когда у банка лицензию не отберут или банк сам не обанкротится) можно такие проценты снимать постоянно в течение неограниченного периода времени. Единственное, что может нарушить данную идиллическую картину, — инфляция, из-за которой деньги обецениваются. Поэтому со времени снимаемые проценты будут всё меньше материальных благ приносить.

Анализ CFA — Как рассчитывать будущую стоимость денежного потока (FV)?

График погашения

В расчете платежей по кредиту при аннуитетных платежах важны не только сумма переплаты и ежемесячный платеж. Следует знать, как уменьшается самый главный критерий – основной долг.

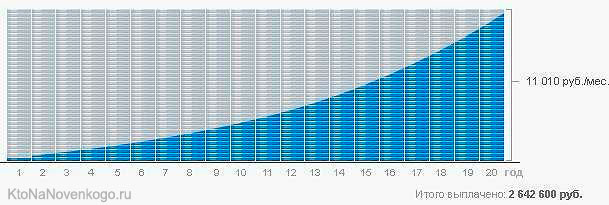
Воспользуемся цифрами из примера выше. В течение всего периода тело долга будет уменьшаться ежемесячно неравномерно. В первый месяц вы заплатите 2 684 рубля, а в последний 34 562. С процентами все наоборот. В первый месяц заплатите 32 250 р., а в последний 372 р. Таким образом, по такому кредиту нельзя допускать просрочек ввиду больших штрафов.

Далее рассмотрим то, как рассчитываются аннуитетные платежи по кредиту. Вы сможете самостоятельно пользоваться формулами для расчета.

Как рассчитать размер платежей по ипотеке с фиксированной процентной ставкой?

Вы планируете приобрести дом стоимостью $120,000, сделав первоначальный взнос в размере $20,000 за счет собственных средств, а также заимствуя остаток суммы по 30-летней ипотеке с ежемесячными платежами по фиксированной процентной ставке.

Первый платеж по ипотеке должен быть осуществлен при t = 1.

Текущая заявленная процентная ставка по ипотечному кредиту составляет 8% при ежемесячном начислении процентов.

Каковы будут ваши ежемесячные платежи по ипотечному кредиту?

Расчет:

Банк будет рассчитывать платежи по ипотечному кредиту таким образом, чтобы при указанной периодической процентной ставке текущая (приведенная) стоимость платежей PV была равна сумме заимствованных средств (в данном случае $100,000).

Имея это в виду, мы можем использовать формулу 11 \( \mathbf {PV = A \left } \), чтобы рассчитать сумму аннуитетного платежа A.

Для этого необходимо разделить текущую (приведенную) стоимость PV на фактор текущей (приведенной) стоимости аннуитета:

PV = $100,000
r_S = 8% = 0.08
m = 12
r_S/m = 0.08/12 = 0.006667
N = 30
mN = 12 * 30 = 360

Фактор приведенной стоимости = \( \mathbf{ 1- {1 \over \left [1 + (r_s / m) r\right]^{mN} } \over r_s / m} \)

= \( \mathbf {1- {1 \over (1.006667)^{360} } \over 0.006667} \)

= 136.283494

A = PV / Фактор приведенной стоимости
= $100,000 / 136.283494
= $733.76

Сумма ипотеки в размере $100,000 эквивалентна 360 ежемесячным платежам в размере $733.76 при заявленной процентной ставке в 8%.

Расчет ипотеки — это относительно простая задача, связанная с определением размера аннуитетного платежа.

Теперь перейдем к проблеме планирования выхода на пенсию.

Эта проблема иллюстрирует сложность ситуации, при которой человек хочет выйти на пенсию с определенным уровнем пенсионных сбережений.

В течение своей жизни обычный человек может сэкономить только небольшую сумму в начале своей карьеры, но в более зрелом возрасте у него обычно появляются более значительные финансовые ресурсы для увеличения пенсионных взносов.

Пенсионные планы часто связаны с неравномерными денежными потоками.

При работе с неравномерными денежными потоками мы максимально используем принцип, согласно которому стоимость денежных потоков, относящихся к одним и тем же моментам времени, является аддитивной — это называется принципом аддитивности денежных потоков.

Сумма займа

Анализ CFA — Эквивалентность приведенной и будущей стоимости денежных потоков

Анализ CFA — Принцип аддитивности денежного потока

Как вычислять обычный аннуитет, то есть FV равных денежных потоков?

Рассмотрим обычный аннуитет с начислением 5% годовых.

Предположим, что у нас есть 5 отдельных депозитов по $1 000, поступающих с равными интервалами, каждый из которых составляет 1 год, причем 1-й платеж происходит при t = 1.

Наша цель — найти будущую стоимость (FV) этого обычного аннуитета после внесения последнего депозита при t = 5. Поскольку все 5 депозитов вносятся с периодичностью в 1 год, последний платеж осуществляется через 5 лет.

Как показывает временная линия на рисунке выше, мы находим будущую стоимость каждого депозита на сумму $1 000 к моменту времени t = 5, используя для каждого депозита формулу FV (2):

FV_N = PV * (1 + r)N.

Стрелки на рисунке выше соответствуют дате каждого депозита от даты 1-го платежа до t = 5 и указывают на расчет будущей стоимости FV для соответствующего депозита.

Например, по 1-му депозиту в размере $1 000 (при t = 1) будут начисляться проценты в течение 4-х последующих периодов.

Используя формулу FV, мы вычисляем будущую стоимость 1-го депозита при t = 5, которая составляет:

$1 000 * (1,05)4 = $1 215,51.

Для всех других платежей мы вычисляем FV аналогичным образом.

Обратите внимание, что мы находим будущую стоимость при t = 5, поэтому последний (5-й) платеж не важен и не отображается на временной линии. Теперь, имея все значения FV при t = 5, мы можем их суммировать, чтобы получить будущую стоимость аннуитета, т.е

всей последовательности равных денежных потоков. Эта сумма составляет $5 525,63

Теперь, имея все значения FV при t = 5, мы можем их суммировать, чтобы получить будущую стоимость аннуитета, т.е. всей последовательности равных денежных потоков. Эта сумма составляет $5 525,63.

Теперь рассмотрим общую формулу аннуитета, в которой:

• A — сумма аннуитета,
• N — количество периодов и
• r — процентная ставка за период.

Мы можем рассчитать будущую стоимость как

FV_N = A * ,

что можно упростить до следующей формулы:

$$\mathbf { FV_N = A \left }$$

FV_N = A * [((1 + r)N -1) / r]  (формула 7)

Выражение в квадратных скобках — это фактор будущей стоимости аннуитета (англ. ‘future value annuity factor’).

Этот коэффициент означает будущую стоимость обычного аннуитета на одну денежную единицу (т.е. на $1 в нашем примере).

Умножение фактора будущей стоимости аннуитета на сумму аннуитета дает будущую стоимость обычного аннуитета.

Для обычного аннуитета, изображенного на рисунке выше, фактор будущей стоимости аннуитета из формулы 7 можно рассчитать как:

[((1.05)5 — 1) / 0.05] = 5.525631.

Если сумма аннуитета A = $1 000, то будущая стоимость аннуитета составляет $1,000 * (5.525631) = $5,525.63, что соответствует вычислению, сделанному ранее.

Следующий пример иллюстрирует, как можно рассчитать будущую стоимость обычного аннуитета, используя формулу 7.

Пример расчета будущей стоимости простого аннуитета.

Предположим, что пенсионный план вашей компании с установленными взносами позволяет вам инвестировать до €20 000 в год. Вы планируете инвестировать €20 000 в год в индексный инвестиционный фонд в течение следующих 30 лет.

Исторически сложилось так, что этот фонд в среднем приносил своим инвесторам 9% в год.

Исходя из того, что вы будете зарабатывать 9% в год, сколько пенсионных средств будет на вашем счете после внесения последнего платежа?

Решение:

Используйте формулу 7, чтобы найти будущую стоимость аннуитета:

A = €20,000
r = 9% = 0.09
N = 30

Фактор FV аннуитета = / r
= / 0.09 = 136.307539.

FV_N = €20,000 * (136.307539) = €2,726,150.77.

Предполагая, что фонд будет зарабатывать в среднем 9% в год, вы получите €2,726,150.77 к моменту выхода на пенсию.

Profi Credit — Нужен только паспорт!

Последствия пандемии

Анализ CFA — Проблемы с применением правила IRR

Анализ CFA — Как интерпретировать процентные ставки?

Пример расчета

Предположим, что нужно провести расчёт ежемесячного платежа по кредиту с аннуитетным графиком погашения под процентную ставку 48% годовых сроком на 4 года на сумму 20 000 000 рублей. Используя приведённую выше формулу расчёта ежемесячного платежа (A = K • S) и коэффициента К, рассчитаем аннуитетный платёж.

Имеем:

1. i= 48%/12 месяцев = 4% или 0,04
2. n = 4 года* 12 месяцев = 48 (месяцев)
3. S = 20 000 000

А = 0,0472 * 20 000 000 = 943 613 рублей.

Таким образом, в течение 4 лет (или 48 месяцев) необходимо будет вносить в банк платёж в сумме 943 613 рублей. Переплата по кредиту за 4 года составит 25 293 422 ( = 943 613 * 48 – 20 000 000).

В первую очередь аннуитетный способ погашения выгоден банку.

Объясняется это тем, что в течение всего срока погашения кредита проценты начисляются на первоначальную сумму кредита. При дифференцированной графике уплата процентов за 100% суммы кредита происходит только в первом месяце (в случае отсутствия отсрочки уплаты основного долга), далее проценты начисляются на остаток, из-за чего итоговая переплата по кредиту окажется меньше.

Для примера, рассчитаем переплату по кредиту, рассмотренному выше, но теперь с дифференцированным графиком погашения. Она составит 19 600 000 рублей. Это на 5 693 422 рубля меньше, чем при аннуитетной схеме.

С другой стороны, погашение задолженности и процентов равными долями удобно кредитополучателю.

Так как ежемесячный платёж является постоянным и не требует уточнения в банке необходимой суммы взноса.

Применение аннуитетного способа погашения, таким образом, обойдётся дороже, но при этом гораздо удобнее.

Теперь давайте попробуем рассчитать ипотеку. Для примера возьмем займ со следующими параметрами

Параметры рассчитываемого кредита
Сумма	1 млн рублей.
Ставка	12%
Срок	60 месяцев
Дата первого платежа	1 сентября 2011.

где Погашение ОД — сумма в погашение тела займаПроценты — сумма процентов по ссуде за месяц.Где сумма ОД — сумма основного долга на дату расчета.Ставка — процентная ставка в текущем периоде. Если было изменение процентной ставки, берется новая ставка.Число дней между датами — разность в днях между датами «Дата текущего платежа» и дата предыдущего платежа.

В нашем примере при первом платеже это делать не нужно.Рассчитаем первый платеж в уплату процентов по указанному выше займу за сентябрь месяц(разнца между датами 31 день).Как видно сумма ОД на первый месяц составляет 1 млн. рублей. Подставим даты, ставки и число дней в году.

Как видно, в счет уплаты процентов должно пойти 10191.78Произведем расчет суммы в погашение тела займа

Теперь рассчитаем сумму основного долга после оплаты первого взноса по ипотеке

Теперь допустим, мы погасили 100000 рублей в августе 2012. Тип погашения — в уменьшение суммы займа. Т.е срок останется тем же, а ежемесячный платеж уменьшится.Попробуем посчитать, сколько будет составлять платеж после учета досрочных погашений. В октябре будет уже новый платеж по займу с учетом досрочки.

Воспользуемся формулой для расчета аннуитетных платежей. Из всех параметров у нас изменилась только сумма основного долга после досрочного погашения в августе она равна

Вычисленная выше сумма и будет сумма кредита после досрочного погашения.Именно исходя из этой суммы и будет рассчитываться ежемесячный аннуитетный платеж после досрочного погашения.

Очевидно срок кредита также изменится, нужно отнять от общего срока число месяцев, прошедшее до досрочного погашения с момента выдачи займа.

Подставим новую сумму в формулу аннуитетного платежа получим новый платеж по займу.

Итоговый расчет

Проверим это с помощью программы кредитный калькулятор

Как видно результат полностью совпадает. Также можно воспользоваться онлайн версией кредитного калькулятора. Там используется указанная выше формула аннуитетного платежа. График кредитного калькулятора может быть использован для сверки расчетов вашего кредита с расчетом банка. Иногда данные могут не совпасть.

Вот к примеру форумла аннуитета в банке ЛевобережныйПо формулеФормула немного другая. Она взята из стандартного ипотечного договора.Вы должны понимать, что досрочное погашение с финансовой точки зрения не всегда выгодно. Предлагаю попробовать калькулятор, определяющий выгодность досрочного погашения.

Преимущества аннуитетных платежей

Коэффициент аннуитета

Коэффициент аннуитета превращает разовый платёж сегодня в платёжный ряд. С помощью данного коэффициента определяется величина периодических равных выплат по кредиту:

K=i⋅(1+i)n(1+i)n−1{\displaystyle K={\frac {i\cdot (1+i)^{n}}{(1+i)^{n}-1}}},

где i{\displaystyle i} — процентная ставка за один период, n{\displaystyle n} — количество периодов на протяжении всего действия аннуитета (количество операций по капитализации процентов). На практике возможны некоторые отличия от математического расчёта, вызванные округлением, а также неодинаковой продолжительностью месяца и года; особенно это касается последнего по сроку платежа.

Предполагается, что выплаты производятся постнумерандо, то есть в конце каждого периода. И тогда величина периодической выплаты A=K⋅S{\displaystyle A=K\cdot S}, где S{\displaystyle S} — величина кредита.

Пример расчёта. Рассчитаем ежемесячную выплату по трехлетнему кредиту суммой 12000 долларов по ставке 6 % годовых. Поскольку выплаты будут производиться каждый месяц, необходимо привести процентную ставку из годового значения к месячному:

100%+6%12−1=1,0612−1≈1,00487−1=,00487=,487%{\displaystyle {\sqrt{100\%+6\%}}-1={\sqrt{1,06}}-1\approx 1,00487-1=0,00487=0,487\%}.

Подставляем в указанную выше формулу следующие значения: i=,00487{\displaystyle i=0,00487}, n=36{\displaystyle n=36}. Полученный коэффициент умножаем на сумму кредита — 12000. Получаем около 364 долларов 20 центов в месяц.

Обычно погашение долга предусматривает ежемесячные или ежеквартальные выплаты, и задаётся годовая процентная ставка i{\displaystyle i}. Если выплаты производятся постнумерандо m{\displaystyle m} раз в год в течение n{\displaystyle n} лет, то точная формула для коэффициента аннуитета:

K=(1+im)k(1+im)k−1⋅(1+im−1)=(1+im−1)⋅(1+i)n(1+i)n−1{\displaystyle K={\frac {({\sqrt{1+i}})^{k}}{({\sqrt{1+i}})^{k}-1}}\cdot ({\sqrt{1+i}}-1)={\frac {({\sqrt{1+i}}-1)\cdot (1+i)^{n}}{(1+i)^{n}-1}}}

или по упрощенной формуле:

K=1+im−11−(1+i)−n{\displaystyle K={\frac {{\sqrt{1+i}}-1}{1-(1+i)^{-n}}}},

где k{\displaystyle k} (всегда показатель степени) — количество периодов = n⋅m{\displaystyle n\cdot m}.

Представленная здесь формула коэффициента аннуитета основана на определении наращенной суммы долга с использованием формулы сложных процентов. Существует формула коэффициента аннуитета, основанная на определении наращенной суммы долга по формуле простых процентов. Кардинальное отличие простых процентов в отсутствии промежуточной капитализации процентов, поэтому при расчёте простыми процентами сначала производится выплата основного долга, а после того, как весь долг выплачен, начинается выплата (капитализация) процентов.

Сначала производится расчёт m=(p+2)2+8pn−(p+2)2p{\displaystyle ={(p+2)^{2}+8pn}}-(p+2)}{2p}}]}

Затем m=2n+mm+1p2m+1p+2{\displaystyle m={\frac {2n+p}{2p+2}}}

X=Km{\displaystyle X={\frac {K}{m}}}

Где n -количество месяцев кредита,

y — годовая процентная ставка

p = y12{\displaystyle y/12} — месячная процентная ставка

K — размер кредита

m — количество месяцев выплаты основного долга

 — целое число от m

X — ежемесячный аннуитетный платеж

Пример. n=12,y=120 %=1.2,p=10 %=0.1,K=100000,

тогда =8, m=8.21052631578947

X=12179.49

Месяц	Платеж	Погашениеосновногодолга	Погашениепроцентов	Основнойдолг	Начислениепроцентов	Накопленныепроценты
			100 000,00
1	12 179,49	12 179,49	0,00	87 820,51	10 000,00	10 000,00
2	12 179,49	12 179,49	0,00	75 641,03	8782,05	18 782,05
3	12 179,49	12 179,49	0,00	63 461,54	7564,10	26 346,15
4	12 179,49	12 179,49	0,00	51 282,05	6346,15	32 692,31
5	12 179,49	12 179,49	0,00	39 102,56	5128,21	37 820,51
6	12 179,49	12 179,49	0,00	26 923,08	3910,26	41 730,77
7	12 179,49	12 179,49	0,00	14 743,59	2692,31	44 423,08
8	12 179,49	12 179,49	0,00	2564,10	1474,36	45 897,44
9	12 179,49	2564,10	9615,38	0,00	256,41	36 538,46
10	12 179,49	0,00	12 179,49	0,00	0,00	24 358,97
11	12 179,49	0,00	12 179,49	0,00	0,00	12 179,49
12	12 179,49	0,00	12 179,49	0,00	0,00	0,00

Досрочное погашение аннуитетного платежа: виды и нюансы

В результате таких действий кредитная организация теряет часть дохода, который был рассчитан при выдаче ссуды. Если клиент сегодня оформил заем, а через две недели его вернул, то банк лишился своей прибыли. Несмотря на это почти все кредиторы предоставляют заемщику такую возможность на определенных условиях.

Для клиента частичное досрочное погашение долга выгодно, так как уменьшится переплата. Например, банк выдал кредит 500 000 руб. и начисляет проценты на эту сумму. Через некоторое время заемщик вернул 100 000 руб. Банк остается в убытке, так как теперь проценты будут начисляться уже на оставшиеся 400 000 руб.

Если вы планируете досрочно погасить аннуитетный кредит, предупредите об этом банк. Срок извещения кредитора указывается в договоре, но обычно за 1 месяц до внесения следующей оплаты. Заявление можно подать как устно, так и в письменной форме. Это зависит от условий сделки.

На дату очередного взноса на счету заемщика должны лежать деньги, которых достаточно для списания всей увеличенной суммы. Банк составит новый аннуитетный график.

Клиент может вернуть себе определенную часть уплаченных процентов по кредиту. Обычно это практикуют, если досрочное погашение произошло в самом начале кредитования.

Первый вариант банки стараются исключить из условий договора, так как он выгоден в первую очередь для клиента.

Решаетесь на досрочное погашение, посчитайте, выгодно ли оно для вас. Кредитные организации вначале стремятся получить от заемщика процентную часть, и только потом основной долг. А при перерасчете станут учитывать остаток тела кредита.

Чтобы сделать правильный выбор, просчитайте на калькуляторе аннуитетных платежей все возможные варианты.

We have updated our privacy policy

Автоматический расчет

Если вы не хотите вникать в тонкости расчетов по данной формуле, можете воспользоваться формой для автоматического расчета платежей. Иначе говоря, онлайн-калькулятором.

Один из подобных калькуляторов можно найти по адресу: http://extloancalculator.com/calculators/simple-annuitetnyjj-kalkulyator-ru.html. Это очень удобно, так как можно не только рассчитать сумму ежемесячного платежа, но и увидеть развернутый график погашения с указанием доли основного долга и процентов по кредиту в каждом периоде.

Есть еще один способ автоматизации расчета аннуитетного платежа. Для этого нужно воспользоваться программой Microsoft Excel. Просто создаем новую страницу и в любой клетке прописываем формулу.

Для этого в выбранной клетке ставим знак «=», далее выбираем специальную функцию ПЛТ и в открывшемся окне вводим параметры:

• ставка – в нашем примере 24% годовых, значит вводим «24%/12» (по количеству месяцев в году);
• кпер – общее количество периодов выплат по займу – «24»;
• пс – приведенная стоимость, т.е. общая сумма по кредиту – «100000»;

Должна получиться такая формула: =ПЛТ(24%/12;24;100000), а результат равен 5287,11.

Наша лучшая кредитная карта

Формула расчета аннуитетных платежей

Размер ежемесячной выплаты рассчитывается исходя из суммы, срока и процентной ставки с использованием коэффициента аннуитета.

Формула коэффициента аннуитета

A = P * (1+P)N / ((1+P)N-1), где

A — коэффициент аннуитета;
P — процентная ставка выраженная десятичной дробью в расчете на период. Например, для случая 12% годовых и ежемесячной выплаты это составит 0.12/12 = 0.01;
N — число периодов гашения займа.

Sa = A * K, где

Sa — аннуитетный платеж;
A — коэффициент аннуитета;
K — кредит.

Формула общей суммы выплат

S = N * Sa = N * A * K, где

S — общая сумма выплат;
Sa — аннуитетный платеж;
N — число периодов гашения (обычно месяцев);
A — коэффициент аннуитета;
K — кредит.

Sp = S — K, где

S — общая сумма выплат;
K — кредит.

Пример 1

Ссуда 100 000 рублей на 5 лет под 12% годовых с ежемесячными выплатами.

В этом случае число периодов погашения N = 5*12 = 60,
процентная ставка на период P = 0.12 / 12 = 0.01.

Коэффициент аннуитета:

A = 0.01 * (1+0.01)60 / ((1+0.01)60-1) = 0.0222444

Аннуитетный платеж:

Sa = 0.0222444 * 100 000 = 2224.44 руб.

Всего выплат:

S = 60 * 2224.44 = 133 466.69 руб.

Сумма процентов (переплата):

Sp = 133 466.69 — 100 000 = 33 466.69 руб.

Пример 2

Ссуда 100 000 рублей на 3 года под 12% годовых с ежемесячными выплатами.

Число периодов гашения N = 3*12 = 36,ставка на период P = 0.12 / 12 = 0.01.

Коэффициент аннуитета:

A = 0.01 * (1+0.01)36 / ((1+0.01)36-1) = 0.0332143

Аннуитетный платеж:

Sa = 0.0332143 * 100 000 = 3321.43 руб.

Всего выплат:

S = 36 * 3321.43 = 119 571.52 руб.

Переплата:

Sp = 119 571.52 — 100 000 = 19 571.52 руб.

Выводы

Видим, что с уменьшением срока займа:

• Аннуитетный платеж растет
• Общая сумма выплат уменьшается
• Переплата уменьшается

В случае досрочного погашения займа величина переплаты уменьшается еще сильнее, см. ниже.

В приведенных примерах условия займа не изменялись. Если сравнивать займы с разными условиями, чтобы понять какой выгоднее, полезно вычислять несколько дополнительных показателей: процент переплаты и эффективную процентную ставку.

Формула расчета процента переплаты

Показывает какую долю от займа составляет переплата:

Pp = Sp / K * 100%, где   

Pp — процент переплаты;
Sp — переплата;
K — кредит;

Для приведенных выше примеров

Пример 1: Pp = 33.47%
Пример 2: Pp = 19.57%

Формула эффективной процентной ставки

Эффективная процентная ставка это процент переплаты, деленный на срок займа, выраженный в годах:

Pэф = Pp / (годы) = Pp / (N / 12)

Pэф — эффективная процентная ставка;
Pp — процент переплаты;
N — число месяцев гашения;